Video: Kotirovka qaydası əvəzinə məhsul qaydasından istifadə edə bilərsinizmi?
2024 Müəllif: Miles Stephen | [email protected]. Son dəyişdirildi: 2023-12-15 23:33
Bunun iki səbəbi var nisbət qaydası bilər gücdən üstün olmaq qayda plus məhsul qaydası fərqləndirməkdə a əmsal : Nəticəni sadələşdirərkən ortaq məxrəcləri qoruyur. Əgər istifadə edirsən güc qayda plus məhsul qaydası , Sən nəticəni sadələşdirmək üçün çox vaxt ortaq məxrəc tapmalıdır.
Eynilə soruşa bilərsiniz ki, məhsul qaydası ilə quotient qaydası arasındakı fərq nədir?
The Məhsul Qaydası a-nın törəməsi olduğunu deyir məhsul iki funksiyanın birinci funksiyası ikinci funksiyanın törəməsi ilə üstəgəl ikinci funksiyanın birinci funksiyanın törəməsidir. The Məhsul Qaydası törəməsi olduqda istifadə edilməlidir əmsal iki funksiyanı götürmək lazımdır.
Həmçinin məhsul qaydasının necə işlədiyini bilirsinizmi? The məhsul qaydası bir neçə və ya bir neçə kiçik funksiyanın vurulması olan funksiyanın törəməsini götürmək istənildikdə hesablamada istifadə olunur. Başqa sözlə, f(x) funksiyası a-dır məhsul funksiyaları varsa bacarmaq g(x)h(x) kimi yazılsın və s. Bu funksiya a məhsul iki kiçik funksiyadan ibarətdir.
Bu şəkildə, biz niyə quotient qaydasından istifadə edirik?
Giriş Hissə Qaydası The əmsal qaydası törəmələrin hesablanması üçün əsas qaydaların sonuncusudur və o, ilk növbədə, əgər nə baş verərsə, onunla məşğul olur. Sən başqa bir funksiyaya bölünmüş funksiyaya malikdir və Sən istəyirəm almaq bunun törəməsi.
Bölmə qaydasının düsturu nədir?
The əmsal qaydası a düstur a-nın törəməsini götürmək üçün əmsal iki funksiyadan ibarətdir. The düstur bildirir ki, f(x)-in g(x)-ə bölünən törəməsini tapmaq üçün aşağıdakıları etməlisiniz: f(x)-in törəməsinin g(x) çarpımını götürün. Sonra həmin hasildən g(x)-in törəməsinin f(x) hasilini çıxarmalısınız.
Tövsiyə:
Məhsul və əmsal qaydasından necə istifadə edirsiniz?
Məhsul Qaydası deyir ki, iki funksiyanın hasilinin törəməsi birinci funksiyanın ikinci funksiyanın törəməsi ilə üstəgəl ikinci funksiyanın birinci funksiyanın törəməsidir. İki funksiyanın bölünməsinin törəməsi alınarkən Məhsul Qaydasından istifadə edilməlidir
Düz olmayan üçbucaqlarda sin və cos istifadə edə bilərsinizmi?
Yan uzunluqları x və y ilə göstərildiyi kimi etiketlənmiş başqa bir düz olmayan üçbucağı nəzərdən keçirək. Yalnız kosinus funksiyasını ehtiva edən faydalı qanun çıxara bilərik. Düzbucaqlı olmayan üçbucağın bucağının və ya tərəfinin ölçüsünü tapmaq üçün kosinuslar qanunundan istifadə edilə bilər, əgər bilirik: üç tərəf və bucaq yoxdur
Məhsul və ya əmsal qaydasından nə vaxt istifadə edəcəyinizi necə bilirsiniz?
Funksiyaların bölgüsü. Beləliklə, hər dəfə iki funksiyanın vurulmasını görəndə məhsul qaydasından, bölünmə halında isə əmsal qaydasından istifadə edin. Əgər funksiyada həm vurma, həm də bölmə varsa, sadəcə olaraq hər iki qaydadan istifadə edin. Əgər ümumi bir tənlik görürsünüzsə, bu, kimi bir şeydir, burada yalnız baxımından bir funksiyadır
Məhsul qaydası ilə zəncir qaydası arasındakı fərq nədir?
Ümumilikdə f(g(x)) kimi 'funksiya funksiyasını' diferensiallaşdırarkən zəncir qaydasından istifadə edirik. Ümumilikdə f(x)g(x) kimi birlikdə vurulmuş iki funksiyanı fərqləndirərkən hasil qaydasından istifadə edirik. Ancaq unutmayın ki, onlar ayrı funksiyalardır: biri digərinin cavabına etibar etmir
Çarpaz məhsul üçün sağ əl qaydasından necə istifadə edirsiniz?
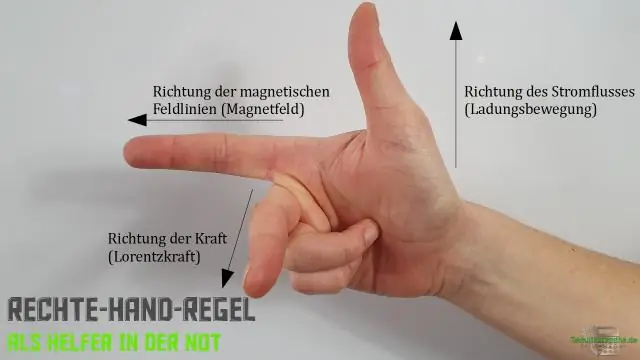
Sağ əl qaydası bildirir ki, vektorların çarpaz hasilinin oriyentasiyası sağ əli yerləşdirmək və quyruqdan quyruğa çevirməklə, sağ əli düzləşdirməklə, onu istiqamətə uzatmaqla və sonra barmaqları bucağın yaratdığı istiqamətdə bükməklə müəyyən edilir. Sonra baş barmaq istiqamətini göstərir