
Mündəricat:
- Müəllif Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Son dəyişdirildi 2025-01-22 16:56.
tapın sahə içərisində kardioid r = 1 + cos θ. Cavab kardioid ürək formasında olduğu üçün belə adlandırılmışdır. Radial zolaqlardan istifadə edərək, inteqrasiyanın hədləri (daxili) r 0-dan 1-ə qədər + cos θ; (xarici) θ 0-dan 2π-ə qədər. Belə ki, sahə edir. 2π 1+cos θ dA = r dr dθ.
Üstəlik, qütb bölgəsinin sahəsini necə tapmaq olar?
r=f(θ) tənliyi ilə α≦θ≦β ilə təyin olunan qütb koordinatlarında rayonun sahəsi A=1 inteqralı ilə verilir. 2 ∫βα[f(θ)] 2 dθ. Aradakı sahəni tapmaq üçün iki qütb koordinat sistemindəki əyrilər üçün əvvəlcə kəsişmə nöqtələrini tapın, sonra müvafiq sahələri çıxarın.
Biri də soruşa bilər ki, Cos 2x-i necə inteqrasiya edirsiniz? The inteqral of cos ( 2x ) (1/2)sin( 2x ) + C, burada C sabitdir.
Burada əyri altındakı sahənin düsturu nədir?
The əyri altındakı sahə iki nöqtə arasında müəyyən inteqral aparılmaqla tapılır. tapmaq üçün altındakı sahə the əyri y = f(x) x = a & x = b arasında, y = f(x) a və b hədləri arasında inteqrasiya edin. Bu sahə verilmiş limitlərlə inteqrasiyadan istifadə etməklə hesablana bilər.
Parametrik tənlikləri necə həll edirsiniz?
Misal 1:
- y=x2+5 tənliyi üçün parametrik tənliklər toplusunu tapın.
- t-ə bərabər dəyişənlərdən hər hansı birini təyin edin. (deyin: x = t).
- Sonra verilmiş tənliyi y=t2+5 şəklində yenidən yazmaq olar.
- Deməli, parametrik tənliklər toplusu x = t və y=t2+5 dir.
Tövsiyə:
Bir obyekt böyüdükcə həcm və səth sahəsi arasında dəyişən əlaqə nədir?
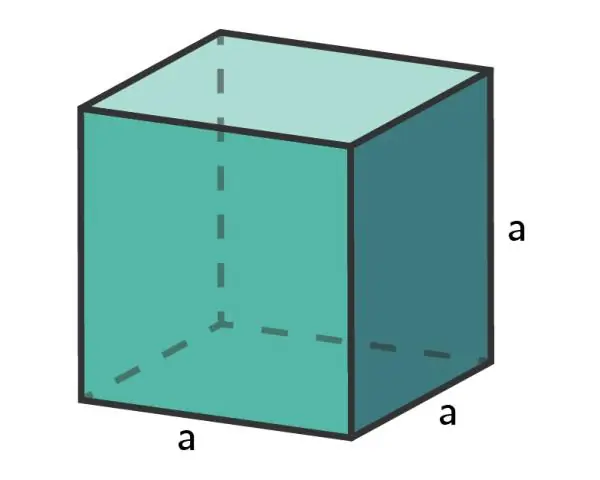
Kub ölçüsü artdıqca və ya hüceyrə böyüdükcə səth sahəsinin həcm nisbəti - SA:V nisbəti azalır. Obyekt/hüceyrə çox kiçik olduqda, onun böyük səth sahəsinin həcm nisbətinə, böyük obyektin/hüceyrə isə kiçik səth sahəsinin həcminə nisbətinə malikdir
Əhali dinamikası sahəsi nədir və populyasiyaları öyrənərkən nə üçün faydalıdır?
Əhali dinamikası, dinamik sistemlər kimi populyasiyaların ölçüsünü və yaş tərkibini və onları hərəkətə gətirən bioloji və ekoloji prosesləri (məsələn, doğum və ölüm nisbətləri, immiqrasiya və emiqrasiya ilə) öyrənən həyat elmləri sahəsidir
Funksiyanızın praktik sahəsi və diapazonu nədir?

'y'nin mümkün qiymətləri diapazon adlanır. Nəzəri sahələr və diapazonlar bütün mümkün həlləri əhatə edir. Praktiki domenlər və diapazonlar müəyyən edilmiş parametrlər daxilində real olmaq üçün həll dəstlərini daraldır
Fırlanma sahəsi nədir?

Fırlanma bir mərkəz ətrafında hərəkət edən cismin hərəkətidir, məsələn, Yer öz oxu ətrafında fırlanır; İnqilab, Ayın Yer ətrafında fırlanması kimi xarici bir nöqtənin ətrafında fırlanma hərəkətidir
Səth sahəsi ilə yanal sahə arasındakı fərq nədir?
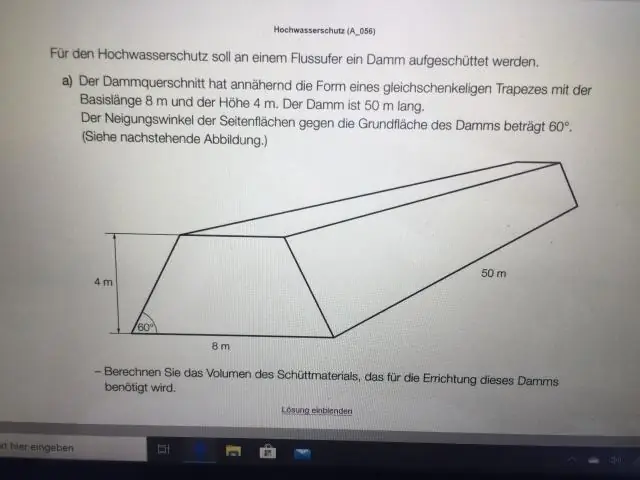
Yan səth sahəsi bazanın sahəsi istisna olmaqla, bütün tərəflərin sahəsidir. İstənilən bərk cismin ümumi səthi bərk cismin bütün üzlərinin sahələrinin cəmidir
