Mündəricat:
Video: Bucaq əlavə postulatı ilə seqment əlavə postulatı arasındakı fərq nədir?
2024 Müəllif: Miles Stephen | [email protected]. Son dəyişdirildi: 2023-12-15 23:33
Seqment əlavəsi postulatı - Əgər B arasında A və C, sonra AB + BC = AC. Əgər AB + BC = AC, onda B olur arasında A və C. Bucaq əlavəsi postulatı – P olarsa içində daxili of ∠, onda ∠ + ∠ = ∠.
Bu baxımdan bucaq əlavəsi postulatı nə deməkdir?
The Bucaq əlavəsi postulatı bildirir ki: Əgər B nöqtəsi daxili hissədə yerləşirsə bucaq AOC, onda.. The postulat iki qoyduğunu təsvir edir bucaqlar onların təpələri ilə yan-yana birlikdə yenisini yaradır bucaq kimin ölçüsü bərabərdir məbləğ iki orijinalın ölçülərinin bucaqlar.
Həmçinin, bucağın ölçüsünü necə tapmaq olar? Bir iletki istifadə etmək üçün ən yaxşı yol ölçü bir bucaq daşıyıcıdan istifadə etməkdir. Bunu etmək üçün, bir şüanı iletki üzərində 0 dərəcə xətti boyunca düzməklə başlayacaqsınız. Sonra, təpəni iletirin orta nöqtəsi ilə düzün. Müəyyən etmək üçün ikinci şüaya əməl edin bucağın ölçülməsi ən yaxın dərəcəyə qədər.
Eynilə, insanlar soruşurlar ki, seqment əlavəsi nəyi ifadə edir?
Həndəsə, Seqment Əlavəsi Postulatı vəziyyətləri ki, 2 nöqtə A və C verildikdə, üçüncü B nöqtəsi xətt üzərində yerləşir seqment AC o zaman və yalnız nöqtələr arasındakı məsafələr AB + BC = AC tənliyini təmin edərsə. The seqment əlavəsi postulatı uyğunluğu üzrə nəticələri sübut etmək üçün çox vaxt faydalıdır seqmentlər.
Bucağı necə ikiyə bölürsən?
Tikinti: ikiyə bölün ∠ABC
- ADDIMLAR:
- Kompas nöqtəsini bucağın təpəsinə qoyun (B nöqtəsi).
- Kompası bucaqda qalacaq istənilən uzunluğa uzatın.
- Qələm verilmiş bucağın hər iki tərəfini (şüalarını) keçəcək şəkildə bir qövs yelləyin.
- Kompas nöqtəsini bucağın yan tərəflərindəki bu yeni kəsişmə nöqtələrindən birinə qoyun.
Tövsiyə:
Osmoz diffuziyası ilə asanlaşdırılmış diffuziya arasındakı fərq nədir?
Suyun bir hüceyrədən digərinə keçdiyi zaman da osmoz baş verir. Digər tərəfdən asanlaşdırılmış diffuziya hüceyrəni əhatə edən mühit hüceyrə daxilindəki mühitdən daha çox ion və ya molekul konsentrasiyasında olduqda baş verir. Molekullar diffuziya qradiyenti səbəbindən ətraf mühitdən hüceyrəyə keçir
Korrelyasiya ilə chi kvadratı arasındakı fərq nədir?
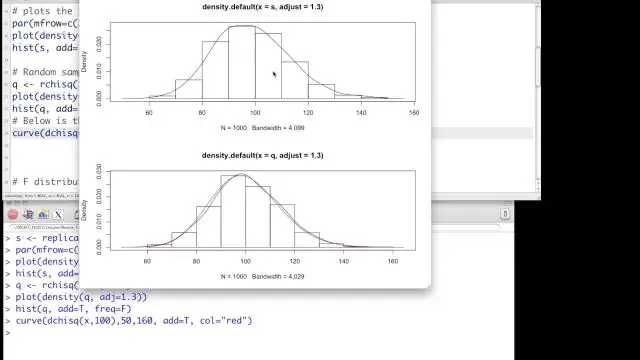
Beləliklə, korrelyasiya iki dəyişən arasındakı xətti əlaqə haqqındadır. Adətən, hər ikisi davamlıdır (və ya təxminən belədir), lakin birinin dixotom olduğu vəziyyət üçün dəyişikliklər var. Ki-kvadrat adətən iki dəyişənin müstəqilliyinə aiddir. Adətən, hər ikisi kateqoriyalıdır
Riyaziyyatda bucaq əlavəsi postulatı nədir?
Bucaq əlavəsi postulatı bildirir ki: Əgər B nöqtəsi AOC bucağının daxili hissəsində yerləşirsə, onda.. Postulat təsvir edir ki, iki bucağın təpələri ilə yan-yana qoyulması ölçüsü ikisinin ölçülərinin cəminə bərabər olan yeni bucaq yaradır. orijinal açılar
Seqment və akkord arasındakı fərq nədir?
Fellər kimi akkordla seqment arasındakı fərq ondan ibarətdir ki, akkord akkordlar yazmaq, seqment isə seqmentlərə və ya bölmələrə bölməkdir
Bucaq postulatı nədir?
Bucaq əlavəsi postulatı bildirir ki: Əgər B nöqtəsi AOC bucağının daxili hissəsində yerləşirsə, onda.. Postulat təsvir edir ki, iki bucağın təpələri ilə yan-yana qoyulması ölçüsü ikisinin ölçülərinin cəminə bərabər olan yeni bucaq yaradır. orijinal açılar