
Mündəricat:
- Müəllif Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Son dəyişdirildi 2025-01-22 16:55.
Lyuisi çəkin ayrı-ayrı atomların simvolları molekul . Atomları hər atomun ətrafında səkkiz elektron (və ya H üçün iki elektron) yerləşdirəcək şəkildə birləşdirin. hidrogen ) mümkün olduğu qədər. Paylaşılan elektronların hər bir cütü a kovalent bağ tire ilə təmsil oluna bilən.
Bununla əlaqədar olaraq, bir birləşmə üçün Lewis strukturunu necə çəkmək olar?
Bu təlimatlar molekullar üçün Lyuis strukturlarını çəkmək üçün Kelter strategiyasını təsvir edir
- Addım 1: Valentlik elektronlarının ümumi sayını tapın.
- Addım 2: Atomları "xoşbəxt" etmək üçün lazım olan elektronların sayını tapın
- Addım 3: Molekuldakı Bağların sayını təyin edin.
- Addım 4: Mərkəzi Atom seçin.
Həm də bilirsiniz, istiqraz sifarişini necə tapırsınız? Molekulda ikidən çox atom varsa, əlaqə sırasını müəyyən etmək üçün bu addımları yerinə yetirin:
- Lyuis strukturunu çəkin.
- İstiqrazların ümumi sayını hesablayın.
- Ayrı-ayrı atomlar arasındakı bağ qruplarının sayını hesablayın.
- Atomlar arasındakı bağların sayını molekuldakı bağ qruplarının ümumi sayına bölün.
Eynilə soruşa bilərsiniz ki, kovalent bağlar hansı quruluşu əmələ gətirir?
Kovalent bağlar elektron sıxlığını paylaşan iki atomu, adətən qeyri-metalları əhatə edir forma güclü qarşılıqlı əlaqə. Kovalent bağlar tək, ikiqat və üçlü daxildir istiqrazlar və müvafiq olaraq 2, 4 və ya 6 elektronun paylaşıldığı siqma və pi bağlanma qarşılıqlı təsirlərindən ibarətdir.
bf3 quruluşu nədir?
Molekulun həndəsəsi BF3 Triqonal Planardır. Kimyaya istinadla, 'Trigonal Planar' ortada bir atomun ətrafında üç atomu olan bir modeldir. Bu, hamısı bir müstəvidə olan periferik atomlara bənzəyir, çünki onların üçü də hər birinin üzərindəki 120° əlaqə bucaqları ilə oxşardır ki, bu da onları bərabərtərəfli üçbucaq edir.
Tövsiyə:
Sərbəst bədən diaqramını necə çəkmək olar?

Sərbəst cisim diaqramını çəkmək üçün biz maraq obyektini çəkirik, həmin obyektə təsir edən bütün qüvvələri çəkirik və bütün qüvvə vektorlarını x- və y-komponentlərinə həll edirik. Problemdə hər bir obyekt üçün ayrıca sərbəst cisim diaqramını çəkməliyik
Bitki hüceyrəsini necə çəkmək olar?

VİDEO Sonra, bir bitkini addım-addım necə çəkmək olar? Addımlar Lazım olanı toplayın. Əsas strukturu ondan çıxan bir xətt ilə düzbucaqlı ilə başlayın. Düzbucaqlının altında bir masa düzəldin (daha sonra qazana çevrilir). Düzbucaqlıdan çıxan xəttə yarpaqları əlavə edin.
Bir dairədə neçə qövs çəkmək olar?
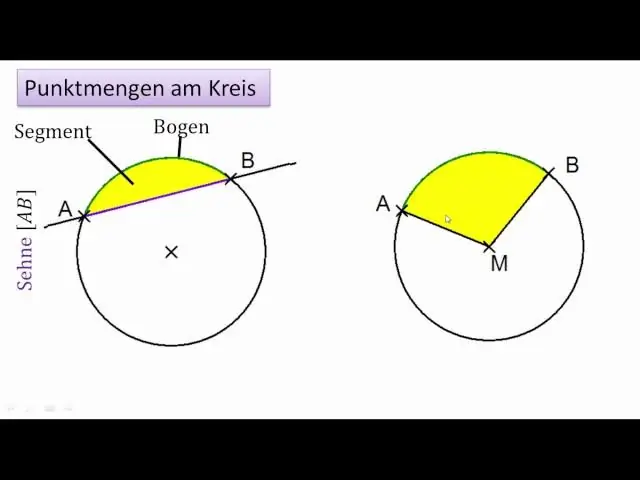
Bir dairənin diametri onu iki bərabər qövsə ayırır. Qövslərin hər biri yarımdairə kimi tanınır. Beləliklə, tam dairədə iki yarımdairə var. Yarımdairələrin hər birinin dərəcə ölçüsü 180 dərəcədir
Bir birləşmənin ion və ya kovalent olduğunu eksperimental olaraq necə təyin etmək olar?

Bir bağın ion və ya kovalent olduğunu müəyyən etmək üçün bir neçə fərqli yol var. Tərifinə görə, ion bağı metal və qeyri-metal arasında, kovalent rabitə isə 2 qeyri-metal arasındadır. Beləliklə, siz adətən sadəcə dövri cədvələ baxırsınız və birləşmənizin metaldan/qeyri-metaldan, yoxsa sadəcə 2 qeyri-metaldan olduğunu müəyyənləşdirirsiniz
Lyuis turşusu Lyuis əsası ilə reaksiya verdikdə hansı növ bağ əmələ gəlir?

Koordinat kovalent rabitə
