
- Müəllif Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Son dəyişdirildi 2025-06-01 05:03.
Sadəcə 2x2 düşünün matris yəni onun tərsinə bənzəyir diaqonal girişlər 1 və ya -1 olmadan. Diaqonal matrislər edəcək. Beləliklə, A və tərs A var oxşar , buna görə də onların xüsusi qiymətləri eynidir. A-nın xüsusi dəyərlərindən biri n olarsa, -in xüsusi qiymətləri onun tərsidir 1/n olacaq.
Həmçinin soruşulur ki, matris öz yerini dəyişdirirmi?
İstənilən kvadrat matris bir sahənin üzərindədir onun transpozisiyasına bənzəyir və istənilən kvadrat kompleksi matris edir oxşar simmetrik kompleksə çevrilir matris.
Eynilə, bütün tərs matrislər oxşardırmı? A və B olarsa oxşar və dönməz , onda A-1 və B-1 olur oxşar . Sübut. ildən hamısı the matrislər var dönməz , hər iki tərəfin tərsini götürə bilərik: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, ona görə də A-1 və B-1 oxşar . A və B olarsa oxşar , hər hansı k = 1, 2, üçün Ak və Bk da belədir.
Bununla əlaqədar olaraq, matris özünə bənzər ola bilərmi?
Yəni İstənilən matris edir özünə bənzəyir : I−1AI=A. Əgər A oxşar B-yə, onda B-dir oxşar A-ya: əgər B=P−1AP, onda A=PBP−1=(P−1)−1BP−1. Əgər A oxşar B=P−1AP vasitəsilə B-yə, C isə oxşar C=Q−1BQ vasitəsilə B-yə, onda A oxşar C-yə: C=Q−1P−1APQ=(PQ)−1APQ.
Matrislər oxşardırsa, bu nə deməkdir?
Xətti cəbrdə iki n-by-n matrislər A və B adlanır oxşar əgər ters çevrilən n-by-n mövcuddur matris P belə. Oxşar matrislər eyni xətti xəritəni iki (bəlkə də) fərqli baza altında təmsil edir, P isə bazanın dəyişməsidir matris.
Tövsiyə:
Matris sözünün mitoxondriya ilə əlaqəsi necədir?
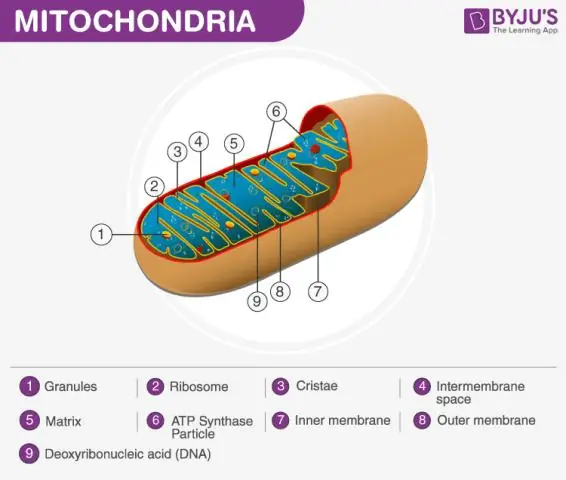
Müəyyən edilmiş mitoxondrial matriks Mitoxondri xarici membrandan, daxili membrandan və matris adlanan geləbənzər materialdan ibarətdir. Bu matris hüceyrənin sitoplazmasından daha viskozdur, çünki tərkibində daha az su var. Bu, ATP adlı enerji molekullarını istehsal edən hüceyrə tənəffüsündə mühüm bir addımdır
Hüceyrədənkənar matris nə edir?

Müxtəlif təbiəti və tərkibinə görə, ECM dəstək təmin etmək, toxumaları bir-birindən ayırmaq və hüceyrələrarası əlaqəni tənzimləmək kimi bir çox funksiyaya xidmət edə bilər. Hüceyrədənkənar matris hüceyrənin dinamik davranışını tənzimləyir
İşığın hansı dalğa kimi xüsusiyyəti bir mühitdən digərinə keçərkən onun istiqamətini dəyişməsinə səbəb olur?

Refraksiya
Bir dairənin hər diametrinin onun radiusunun yarısı olduğu doğrudurmu?

Xeyr, bir dairənin diametri onun radiusundan iki dəfə çoxdur
Bir cismi qızdırdıqda onun kütləsi necə olur?

Bir cismin qızdırılması maddənin kütləsini deyil, yalnız həcmini dəyişir. Kütlə sabitdirsə və həcm artarsa, sıxlıq azalacaq. Temperaturun artması ilə həcm azalırsa, sıxlıq artacaq
