
- Müəllif Miles Stephen [email protected].
- Public 2023-12-15 23:33.
- Son dəyişdirildi 2025-01-22 16:56.
Domen məhdudiyyətlər a rasional funksiya məxrəci sıfıra bərabər qoyub həll etməklə təyin etmək olar. Məxrəcin sıfıra bərabər olduğu x - qiymətləri var təkliklər adlanır və var domenində deyil funksiyası.
Eynilə, rasional funksiyalar nə üçün vacibdir?
Əhəmiyyəti. " Rasional funksiya " a verilən addır funksiyası polinomların əmsalı kimi təqdim oluna bilən a rasional ədəd tam ədədlərin bir hissəsi kimi ifadə edilə bilən ədəddir. Rasional funksiyalar təchizatı vacibdir nümunələrdir və bir çox kontekstdə təbii olaraq baş verir.
Eynilə, rasional funksiyaların dönüş nöqtələri varmı? 4 Xülasə. n dərəcə çoxhədli var ən çox n real sıfır və n−1 dönüş nöqtələri . A rasional funksiya a funksiyası f(x)=P(x)Q(x), f (x) = P (x) Q (x) formasında, burada P(x) və Q(x) var hər iki polinom.
Həmçinin sual yaranır ki, rasional funksiya nümunəsi nədir?
Nümunələr of Rasional funksiyalar The funksiyası R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) a rasional funksiya x^2 + 4x - 1 ədədi çoxhədli və məxrəc olduğu üçün 3x^2 - 9x + 2 də çoxhədlidir.
Rasional funksiyaların xüsusiyyətləri hansılardır?
İki mühüm xüsusiyyətləri hər hansı rasional funksiya r(x)=p(x)q(x) r (x) = p (x) q (x) istənilən sıfırlar və şaquli asimptotlardır. funksiyası ola bilər. Bu cəhətləri a rasional funksiya müvafiq olaraq pay və məxrəcin sıfır olduğu yerlə sıx bağlıdır.
Tövsiyə:
Funksiyaların parametrləri ailələri və qrafiklərin təsvirləri necə əlaqəlidir?

Funksiya ailələri, formanın ən əsas nümunəsi olan ana funksiya ilə tanış olduğunuz zaman onların qrafikini asanlaşdıran oxşarlıqları olan funksiyalar qruplarıdır. Parametr müəyyən bir tənlik yaratmaq üçün müəyyən bir dəyər alan ümumi tənlikdə dəyişəndir
Xüsusiyyət nəzəriyyəsinin məhdudiyyətləri nələrdir?

Xarakter nəzəriyyələrinin başqa bir məhdudiyyəti odur ki, onlar ölçmək üçün şəxsi müşahidələr və ya subyektiv öz-özünə hesabatlar tələb edir, fərdlərin öz davranışlarını bilmək üçün kifayət qədər introspektiv olmasını tələb edir. Xüsusiyyət nəzəriyyələri fərdlərin necə davrana biləcəyi haqqında məlumat versə də, niyə belə davrana biləcəyini izah etmir
Ekoloji piramidaların məhdudiyyətləri nələrdir?

Ekoloji piramidaların məhdudiyyətləri bunlardır: Qida zəncirinin əsas hissəsi olan parçalayıcılara heç bir trofik səviyyədə yer verilmir. Eyni növdən olan orqanizmlər bir və ya bir neçə trofik səviyyədə mövcud ola bilər, lakin eyni səviyyədə hesab olunur
Rasional ifadə üçün məhdudiyyətləri niyə və nə vaxt məhdudiyyətlər bildiririk?

Biz məhdudiyyətləri bildiririk, çünki bu, x-in bəzi qiymətlərində tənliyin qeyri-müəyyən olmasına səbəb ola bilər. Rasional ifadələr üçün ən ümumi məhdudiyyət N/0-dır. Bu o deməkdir ki, sıfıra bölünən istənilən ədəd müəyyən edilməmişdir. Məsələn, f(x) = 6/x² funksiyası üçün x=0 əvəz etdikdə bu, müəyyən edilməmiş 6/0 ilə nəticələnəcək
AutoCAD-də ölçülü məhdudiyyətləri necə tətbiq edə bilərəm?
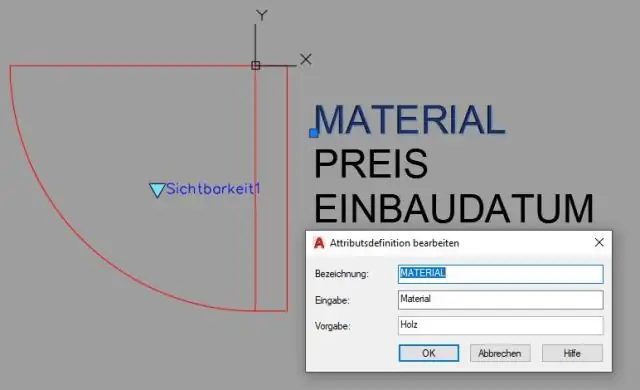
Bu addımlar ölçülü məhdudiyyətlərin sadə nümunəsini təqdim edir: Yeni rəsmə başlayın və Lentin Parametrik nişanını cari edin. Snap, Ortho və Osnap kimi vəziyyət çubuğunda müvafiq dəqiq rəsm vasitələrini yandırın. Dəqiq texnikanı tətbiq etməklə kifayət qədər dəqiq həndəsə çəkin
